In this article, you’ll find a tool that determines the wire size in AWG and mm² that you need to connect your battery to the inverter for you.
If you’re interested in how the tool works or would like to do your calculations manually, I’ll also explain how this works.
Battery to inverter wire size calculator
The battery to inverter wire size calculator below will provide the size of the Copper wire that you need in AWG (American Wire Gauge) and mm² (square millimeters) based on:
- The Continuous Power rating of the inverter (in Watts).
- The voltage of the battery bank (in Volts).
- The distance between the battery bank and the inverter (in feet).
- The ambient temperature of the room in which the wire will be located.
The wire size provided by the calculator will ensure a maximum voltage drop equal to or less than 3% (minimal power losses) even if the temperature of the wire goes up to 194°F(90°C).
Battery to inverter wire size calculator
Please note that the calculator takes the following American National Electrical Codes (2023’s edition) into consideration:
- NEC 706.30
- NEC 210.19
- NEC 110.14
- NEC 310.16 and 310.15 (B)
To make this more comprehensive, here are 2 examples:
Example 1:
In this example, let us make the following assumptions:
- Our inverter is rated at 700 Watts of power.
- Our battery is rated at 12V.
- The (one-way) distance between the terminals of the inverter and the terminals of the battery is 10 feet.
- The ambient temperature of the room in which the battery and the inverter are situated does not exceed 30°C (86°F).
Let’s submit these values and see what wire size the calculator recommends:
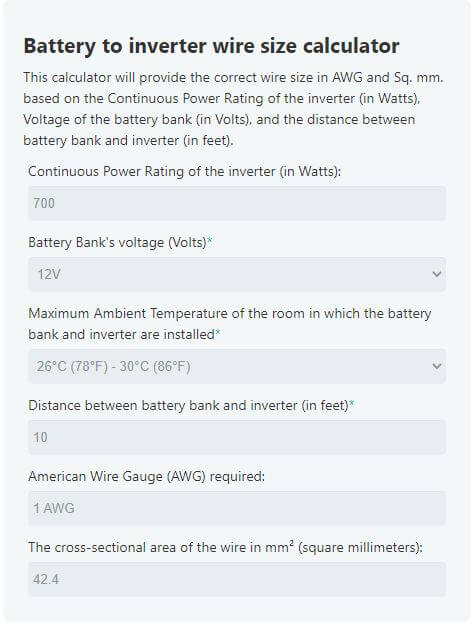
According to the calculator, for a maximum voltage drop of 3%, we would require a 1 AWG copper wire. This means that we would need 20 feet of 1 AWG (42.4mm²) wire. 10 feet of wire from positive to positive, and another 10 feet of wire from negative to negative.
Example 2:
For this example, let’s make the following assumptions:
- Our inverter is rated at 1500 Watts of power.
- Our battery is rated at 48V.
- The (one-way) distance between the terminals of the inverter and the terminals of the battery is 5 feet.
- The ambient temperature of the room in which the battery and the inverter are situated does not exceed 25°C (77°F).
The calculator recommends the following:
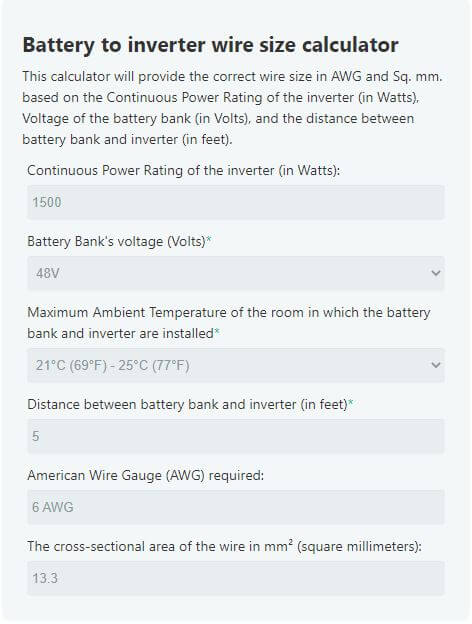
According to the calculator, for a maximum voltage drop of 3%, we would require a 6 AWG copper wire. This means that we would need 10 feet of 6 AWG (13.3mm²) wire. 5 feet of wire from positive to positive, and another 5 feet of wire from negative to negative.
What size wire from the battery to inverter?
When sizing the wire between your battery and the inverter, you’ll need to ensure 2 things:
- The ampacity of the wire you’ll be using is 1.25 higher than the maximum amount of current (Amps) your inverter is capable of pulling from the battery
- The voltage drop across the wire does not exceed 3%
To make this easier to understand, we’ll divide this wire sizing process into 2 parts.
Part 1: Wire ampacity and the 1.25 NEC rule
When sizing a wire, the number one priority is to make sure the wire is capable of handling the amount of current (in Amps) that you’re asking it to conduct. The amount of current that a wire can safely conduct is referred to as Ampacity (in Amps).
To make sure this is the case, the National Electrical Code (NEC 706.30) states that the wire should have an ampacity of not less than 125% of the Maximum Current. So, what is the Maximum Current?
In the same NEC article, the maximum current is defined as the continuous inverter input current rating when the inverter is producing rated power at the lowest input voltage. This can be translated into the following formula:
Maximum Current (Amps) = (Inverter’s Continuous Power rating (Watts) ÷ Lowest Input Voltage (Volts)) ÷ Inverter Efficiency (%) @ max. load
Let me unpack that by providing an example:
Consider an inverter that has a continuous power rating of 1000 Watts. Let us now assume the inverter is connected to a battery bank that has a nominal voltage rating of 24 Volts.
Since Watts = Amps x Volts, and Amps = Watts/Volts, if we know the maximum amount of power that can be pulled out of the battery, and we know the lowest voltage at which that amount of power is being used, we can deduce the maximum amount of current that can be pulled out of the battery.
Let me explain.
We know that our inverter can at most produce 1000 Watts of power at its output. These 1000 Watts that the inverter can produce at its output will be coming from the battery.
However, since inverters are generally only about 85% efficient at maximum load, in order for the inverter to produce 1000W at its output, it will need to pull more than 1000 watts of power from the battery:
Maximum Power that can be drawn from the battery (Watts) = Inverter’s Continuous Power rating (Watts) ÷ Inverter Efficiency (%)
Maximum Power that can be drawn from the battery (Watts) = 1000 Watts ÷ 85%
Maximum Power that can be drawn from the battery (Watts) = 1000 Watts ÷ 0.85
Maximum Power that can be drawn from the battery (Watts) = 1176.4 Watts
Now, we know that the inverter can – at most – pull 1176.4 Watts from the battery. If we divide this value by the lowest voltage of the battery, we can determine the maximum amount of current (in Amps) that the inverter is capable of pulling from the battery.
So, what is the lowest voltage of the battery?
The voltage of a battery correlates directly with its State of Charge (SoC).
For example, even though a 12V battery is rated at 12 Volts, it is a nominal rating. The actual voltage of the battery can go as low as 10 Volts when its discharged. And even at 10 Volts, the inverter is still going to pull the same amount of power if it has to.
By default, most inverters are designed to disconnect the battery at:
- 10 Volts if the battery bank is rated at 12V
- 20 Volts if the battery bank is rated at 24V
- 40 Volts if the battery bank is rated at 48V
However, if the inverter is programmable, or if a Low Voltage Disconnect device is used (such as Victon’s BatteryProtect), and you increase the voltage at which the battery is disconnected, you can instead use that voltage value to calculate the maximum current.
For simplicity, we’ll just assume our 24V battery bank’s voltage is allowed to go as low as 20 Volts. So we’ll just use this voltage value to determine the maximum current we’re looking for:
Maximum Current (Amps) = 1176.4 Watts ÷ 20 Volts
Maximum Current (Amps) = 58.8 Amps
Now we know that our 1000W inverter will – at most – pull 58.8 Amps out of the battery.
As mentioned above, the NEC tells us that the wire’s ampacity should be no less than 125% (or 1.25 times) of the maximum current (58.8 Amps). This can be translated into the following formula:
The ampacity of the wire (Amps) greater than or equal to Maximum Current (Amps) x 1.25
The ampacity of the wire (Amps) greater than or equal to 58.8 Amps x 1.25
The ampacity of the wire (Amps) greater than or equal to 73.5 Amps
However, before we start looking for which wire gauge can safely conduct 73.5 Amps, we need to consider one more factor: The ambient temperature of the room in which the wire will be operating.
This is because the higher the room temperature, the fewer the amps the wire can safely conduct.
For example, a 6AWG THW copper wire can handle up to 65 Amps of current at a room temperature of 30°C (86°F). However, the same copper wire gauge can only safely handle up to 57.2 Amps of current if the room temperature goes up to 40°C (86°F).
To account for ambient temperatures higher (or lower) than 30°C (86°F), you’ll need to multiply the ampacity of the wire at an ambient temperature of 30°C (86°F) provided in NEC table 310.16, by the appropriate temperature correction factor provided in the NEC table 310.15 (B) (1) (1).
We can do this in 2 steps:
- Find the wire gauge using the ampacity table
- Multiply the ampacity of the wire by the correction factor to see if the wire can handle the amps at maximum ambient temperature
First, here are the Ampacities of different copper wire sizes, for different insulation temperature ratings, at an ambient temperature of 30°C (86°F), provided in the NEC table 310.16:
| Copper Wire Size | 60°C(140°F):
Types TW & UF |
75°C(167°F):
Types RHW, THHW, THW, THWN, XHHW, XHWN, USE, ZW |
90°C(194°F):
Types TBS, SA, SIS, FEP, FEPB, MI, PEA, RHH, RHW-2, THHN, THHW, THW-2, THWN-2, USE-2, XHH, XHHW, XHHW-2, XHWN, XHWN-2, XHHN, Z, ZW-2 |
| 14 AWG | 15 A | 20 A | 25 A |
| 12 AWG | 20 A | 25 A | 30 A |
| 10 AWG | 30 A | 35 A | 40 A |
| 8 AWG | 40 A | 50 A | 55 A |
| 6 AWG | 55 A | 65 A | 75 A |
| 4 AWG | 70 A | 85 A | 95 A |
| 3 AWG | 85 A | 100 A | 115 A |
| 2 AWG | 95 A | 115 A | 130 A |
| 1 AWG | 110 A | 130 A | 145 A |
| 1/0 AWG | 125 A | 150 A | 170 A |
| 2/0 AWG | 145 A | 175 A | 195 A |
| 3/0 AWG | 165 A | 200 A | 225 A |
| 4/0 AWG | 195 A | 230 A | 260 A |
Notice that there are 3 columns in the table (60°C through 90°C), with each column specifying different ampacities for the same wire gauge. So, which column should you use?
When trying to determine the size of the wire, NEC 110.14 (C) tells us that:
- For equipment rated 100 Amps or less, the ampacity of the wire should be based on the 60°C column
- For equipment rated for more than 100Amps, the ampacity of the wire should be based on the 75°C column
This is because the terminals of your battery bank, inverter, and the overcurrent protection device (fuse or breaker) might not be able to withstand the temperature that the wire is rated for.
So, unless all of the components that are going to be connected to the wire are explicitly rated for 75°C or more, you should use the 60°C column.
Since our current is 73.5 Amps, and for simplicity, we’ll use the 60°C column.
According to the table, a 3 AWG copper wire can handle up to 85 Amps without exceeding 60°C. So, until now, we’ve determined that we would need a 3 AWG copper wire.
However, again, this is just to size the wire, this does not mean we have to use a copper wire that is rated for 60°C but to ensure the terminals of the equipment don’t get too hot. In fact, the insulation temperature rating of the wire used in applications like these will be 75°C or more.
Now, let us assume we’ll be using a TWH (Thermoplastic high heat-resistant and water-resistant) wire, which has insulation rated for 75°C.
All we need to do now is use one of the following temperature correction factors to make sure our 3 AWG wire can still handle the current without exceeding 60°C:
These temperature correction factors are provided in NEC table 310.15 (B) (1) (1):
| Ambient Temperature | 60°C(140°F):
Types TW & UF |
75°C(167°F):
Types RHW, THHW, THW, THWN, XHHW, XHWN, USE, ZW |
90°C(194°F):
Types TBS, SA, SIS, FEP, FEPB, MI, PEA, RHH, RHW-2, THHN, THHW, THW-2, THWN-2, USE-2, XHH, XHHW, XHHW-2, XHWN, XHWN-2, XHHN, Z, ZW-2 |
| 10°C (50°F) or less | 1.29 | 1.2 | 1.15 |
| 11°C (51°F) – 15°C (59°F) | 1.22 | 1.15 | 1.12 |
| 16°C (60°F) – 20°C (68°F) | 1.15 | 1.11 | 1.08 |
| 21°C (69°F) – 25°C (77°F) | 1.08 | 1.05 | 1.04 |
| 26°C (78°F) – 30°C (86°F) | 1 | 1 | 1 |
| 31°C (87°F) – 35°C (95°F) | 0.91 | 0.94 | 0.96 |
| 36°C (96°F) – 40°C (104°F) | 0.82 | 0.88 | 0.91 |
| 41°C (105°F) – 45°C (113°F) | 0.71 | 0.82 | 0.87 |
| 46°C (114°F) – 50°C (122°F) | 0.58 | 0.75 | 0.82 |
| 51°C (123°F) – 55°C (131°F) | 0.41 | 0.67 | 0.76 |
| 56°C (132°F) – 60°C (140°F) | – | 0.58 | 0.71 |
| 61°C (141°F) – 65°C (149°F) | – | 0.47 | 0.65 |
| 66°C (150°F) – 70°C (158°F) | – | 0.33 | 0.58 |
Now, let us assume that we’ll be installing the wire (along with the battery bank and inverter) in a room in which the ambient temperature can get as high as 104°F(40°C).
Again, even though we’ll be using a THW wire rated for 75°C, we’ll still need to use the 60°C column of table 310.15 (B)(1)(1). For an ambient temperature of 104°F(40°C), the table specifies a correction factor of 0.82.
Let’s multiply the ampacity of our wire (@ an insulation temperature rating of 60°C) by 0.82 and determine the ampacity of the wire at an ambient temperature of 104°F(40°C):
Wire Ampacity (@ 40°C/104°F) = Wire Ampacity (@ 30°C/86°F) x Temperature Correction Factor
Wire Ampacity (@ 40°C/104°F) = 85 Amps x 0.82
Wire Ampacity (@ 40°C/104°F) = 69.7 Amps
If the ambient temperature gets to 104°F(40°C), our wire 3 AWG can only handle up to 69.7 Amps of current before it starts exceeding 60°C. This can be unsafe for other system components.
To correct this, we’ll need to use a 2 AWG copper wire instead of a 3 AWG. The ampacity of a 2 AWG copper wire (@ an insulation temperature rating of 60°C and maximum ambient temperature of 86°F/30°C) is 95 Amps. Let’s use the correction factor to see if a 2 AWG wire is enough:
Wire Ampacity (@ 40°C/104°F) = Wire Ampacity (@ 30°C/86°F) x Temperature Correction Factor
Wire Ampacity (@ 40°C/104°F) = 95 Amps x 0.82
Wire Ampacity (@ 40°C/104°F) = 77.9 Amps
So, even if the ambient temperature of the room goes up to 104°F(40°C), our 2 AWG copper wire can handle up to 77.9 Amps of current without exceeding the 60°C limit.
Therefore, the wire we use between our battery bank and inverter cannot be any smaller than 2 AWG (33.6mm²).
Now, we need to account for the voltage drop. This brings us to part 2.
Part 2: Determining the wire size based on voltage drop
The length and thickness of a wire determine how resistive it’s going to be. The more resistive the wire, the more energy it’s going to dissipate into heat. In other words, the more resistive the wire is, the more energy is going to be lost.
These energy losses can be measured by comparing the voltage at the terminals of the battery bank, to the voltage at the input terminals of the inverter. The difference between these 2 values is referred to as the Voltage Drop.
For example, if the voltage at the terminals of the battery bank is 12 Volts, but the voltage at the input terminals of the inverter is 10.8 Volts, the voltage drop is 1.2 Volts.
For a 12V system, a 1.2V voltage drop means a 10% voltage drop, which then translates into 10% losses in power and energy, which is very inefficient. As a rule of thumb, the voltage drop should not exceed 3%.
So, how do you limit the voltage drop to 3%?
For pure copper conductors, and a voltage drop limited to 3%, the relationship between wire thickness, wire length, the current going through the wire, and voltage drop can be represented via the following formula:
Wire thickness (in Circular Mills) = (12.96 x Maximum Current (Amps) x 2 x One-Way Wire Length (feet)) ÷ (0.03 x Lowest Voltage)
If you know:
- The maximum amount of current that’s going to flow through the wire
- The one-way distance between the terminals of the battery bank and the terminals of the inverter
- The lowest voltage of your battery bank
You could calculate how thick the copper wire should be in order for the voltage drop not to exceed 3%.
To understand this better, let’s follow up on our previous example.
We know that our inverter is rated at 1000 Watts, but again, since inverters are only 85% efficient at max. load, the inverter is capable of drawing more than 1000 Watts of power:
Maximum Power that can be drawn from the battery (Watts) = Inverter’s Continuous Power rating (Watts) ÷ Inverter Efficiency (%)
Maximum Power that can be drawn from the battery (Watts) = 1000 Watts ÷ 85%
Maximum Power that can be drawn from the battery (Watts) = 1000 Watts ÷ 0.85
Maximum Power that can be drawn from the battery (Watts) = 1176.4 Watts
We also know that our battery bank is rated at 24 Volts. We can then calculate the maximum current that can be drawn from the battery at its lowest voltage:
Maximum Current (Amps) = 1176.4 Watts ÷ 20 Volts
Maximum Current (Amps) = 58.8 Amps
Now let’s say that – in our setup – the terminals of the battery bank are going to be 6 feet away from the terminals of the inverter. This means that our positive conductor is going to be 6 feet long, and our negative conductor is going to be 6 feet long.
So, these are the values we’re going to use in our formula:
- Maximum Current: 58.8 Amps
- The one-way distance: 6 feet
- The lowest voltage of the battery bank: 20 Volts
Now we can calculate the necessary thickness of the copper wire (in circular mills):
Wire thickness (in Circular Mills) = (12.96 x Maximum Current (Amps) x 2 x One-Way Wire Length (feet)) ÷ (0.03 x Lowest Voltage)
Wire thickness (in Circular Mills) = (12.96 x 58.8 x 2 x 6) ÷ (0.03 x 20)
Wire thickness (in Circular Mills) = (9144.57) ÷ (0.6)
Wire thickness (in Circular Mills) = 15240.96 C.M
Now that we know the thickness of our wire in circular mills, we can use the following table to determine the size of the wire in AWG or mm²:
| Wire size (AWG) | Wire size (Circular Mills) | Wire size (mm²) |
| 14 AWG | 4110 | 2.1 |
| 12 AWG | 6530 | 3.3 |
| 10 AWG | 10380 | 5.3 |
| 8 AWG | 16510 | 8.4 |
| 6 AWG | 26240 | 13.3 |
| 4 AWG | 41740 | 21.1 |
| 3 AWG | 52620 | 26.7 |
| 2 AWG | 66360 | 33.6 |
| 1 AWG | 83690 | 42.4 |
| 1/0 AWG | 105600 | 53.5 |
| 2/0 AWG | 133100 | 67.4 |
| 3/0 AWG | 167800 | 85 |
| 4/0 AWG | 211600 | 107.2 |
Our calculations have shown that the copper wire’s thickness in C.M needs to be at least 15240.96 in order for the voltage drop not to exceed 3%. From the table, you can see that an 8 AWG wire is 16510 C.M, which is more than enough.
Now, even though we only need an 8 AWG to limit the voltage drop to 3%, in the previous section, using the NEC codes and tables, we have determined that our wire cannot be any smaller than 2 AWG.
Therefore, we’ll need to use a 2 AWG wire.
In a scenario where the distance between our battery bank and inverter is greater, we might have been required to use a larger wire size than 2 AWG.
For example, let’s say that – for some reason – the one-way distance between our battery bank and inverter is 30 feet instead of 6 feet. For this new distance, the thickness of the wire in C.M becomes:
Wire thickness (in Circular Mills) = (12.96 x Maximum Current (Amps) x 2 x One-Way Wire Length (feet)) ÷ (0.03 x Lowest Voltage)
Wire thickness (in Circular Mills) = (12.96 x 58.8 x 2 x 30) ÷ (0.03 x 20)
Wire thickness (in Circular Mills) = (45722.88) ÷ (0.6)
Wire thickness (in Circular Mills) = 76204.8 C.M
In this particular case, a 2 AWG (52620 C.M) wire would not be enough. We would instead need to use a 1 AWG wire.
Now, if you don’t feel like going through this process yourself, the calculator at the beginning of this article will do all of these calculations for you, all you have to do is enter the right specs of your system.
Related Topics:
What size fuse between battery and inverter?
What size wire between solar charge controller and battery?
Thank you for all this. However, for battery cable sizing below 50volts I think you can use welding cable to achieve better carrying capacity relative to size. 1/0 welding cable made in accordance with sae j1127 will carry 350 amps continuous, as opposed to 170 amps for 90 degree thhn under the NEC.